How to find x and y intercepts is a fundamental skill in mathematics that enhances your ability to analyze and graph equations. These intercepts indicate where a graph crosses the axes and provide critical insights into the function’s behavior. This guide will walk you through the methods for finding both x and y intercepts, offering clear examples and practical tips. Mastering these techniques will improve your graphing accuracy and mathematical analysis.
Finding x and y intercepts is a crucial skill in mathematics, particularly in algebra and graphing. These points, where a line or curve intersects the x or y axis, provide valuable information about equations and their graphical representations. Understanding how to find x and y intercepts can help students and professionals alike in various fields, from economics to physics, where graphing and analyzing functions are essential.
This guide will walk readers through the process of finding x and y intercepts step by step. We’ll start by explaining what these intercepts are and why they matter. Then, we’ll dive into the methods for finding x-intercepts, followed by techniques to determine y-intercepts. Along the way, we’ll share helpful tips and tricks to make the process easier and more efficient. By the end, readers will have a solid grasp of how to find x and y intercepts with confidence.
How to Find X and Y Intercepts: Understanding the Basics
Definition of X-intercept
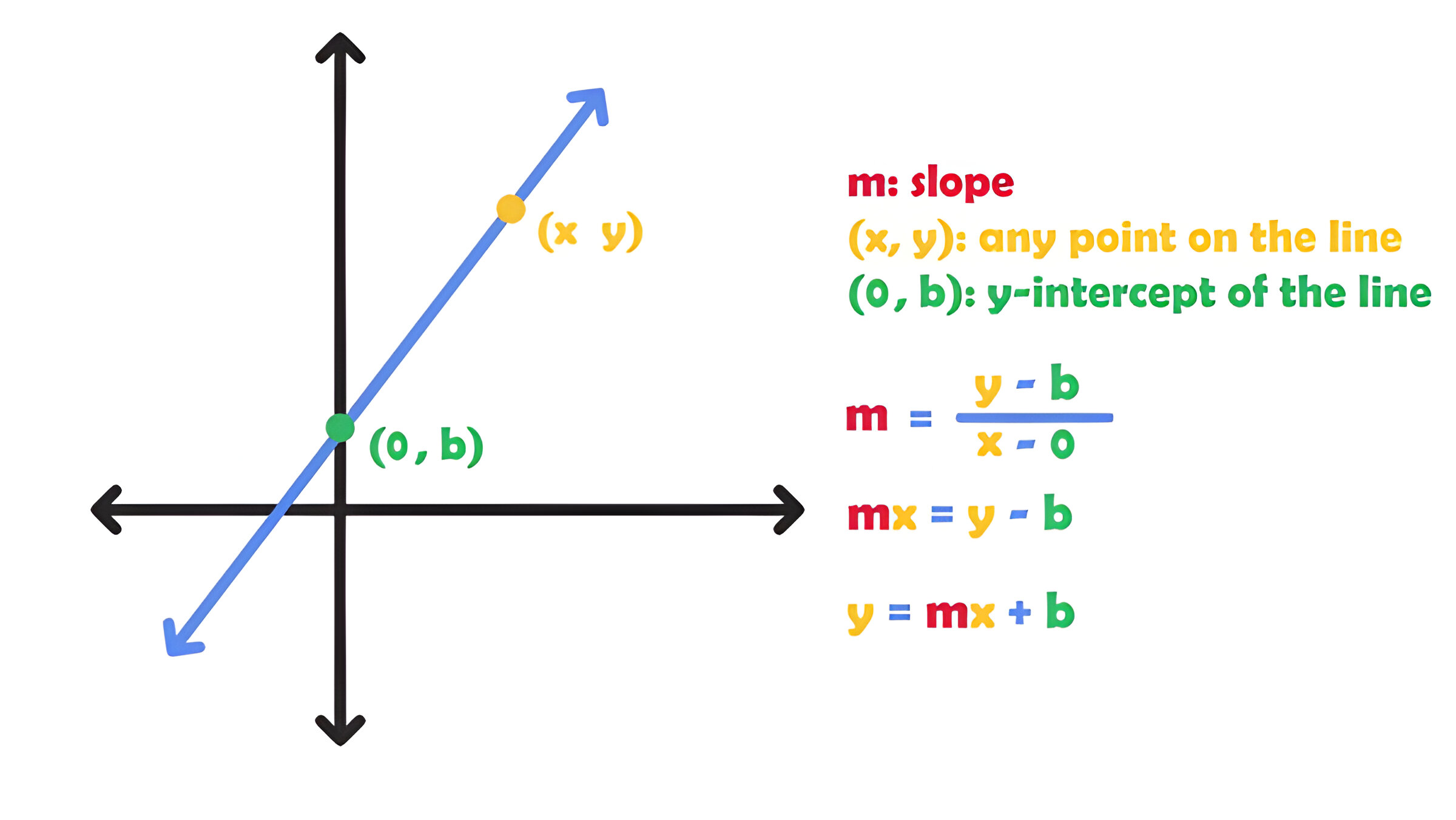
The x-intercept is the point where a graph intersects the x-axis. At this point, the y-coordinate is always zero. To find the x-intercept, one needs to set y equal to zero and solve for x. This process helps determine where the graph crosses the horizontal axis.
Definition of Y-intercept
Similarly, the y-intercept is the point where a graph intersects the y-axis. At this point, the x-coordinate is always zero. To find the y-intercept, one sets x equal to zero and solves for y. This calculation reveals where the graph crosses the vertical axis.
Importance in graphing
Understanding x and y intercepts has a significant role in graphing and analyzing functions. These points provide valuable information about equations and their graphical representations. Here’s why they are crucial:
- Starting point: The y-intercept often represents the initial value or starting point of a function. For instance, in a linear equation y = mx + b, the y-intercept (b) is the constant term that affects the dependent variable regardless of the independent variable (x).
- Baseline information: X and y intercepts help identify the baseline or initial conditions of a relationship depicted in a graph. This information is particularly useful in various fields, such as economics and physics.
- Graph sketching: Knowing the intercepts allows for quick and accurate graph sketching. By plotting these points and connecting them with a straight line, one can easily graph linear equations.
- Equation analysis: Intercepts aid in interpreting the meaning and implications of equations. They can indicate minimum values, thresholds, or starting points relevant to the phenomenon being studied.
- Comparison tool: Intercepts serve as reference points for comparing values of dependent variables across different graphs or conditions, especially when independent variable ranges differ.
By mastering the concept of x and y intercepts, students and professionals can enhance their ability to analyze and interpret graphs effectively. This skill proves invaluable in various disciplines where graphing and function analysis play a significant role.
How to Find X and Y Intercepts: Finding X-Intercepts Step-by-Step
To find the x-intercepts of a graph, one needs to determine where the line or curve crosses the x-axis. This process involves setting y to zero and solving for x. Let’s explore this method step by step.
Setting Y to Zero
The x-intercept is the point where a graph intersects the x-axis. At this point, the y-coordinate is always zero. To find the x-intercept, one must set y equal to zero in the equation of the line or curve. This step is crucial because it represents the condition where the graph touches or crosses the x-axis.
Solving for X
Once y is set to zero, the next step is to solve the equation for x. The method of solving depends on the type of equation:
- For linear equations (y = mx + b):
-
- Set y = 0
- Solve the resulting equation for x
- The solution gives the x-coordinate of the x-intercept
- For quadratic equations (y = ax² + bx + c):
-
- Set y = 0
- Use the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a
- The solutions give the x-coordinates of the x-intercepts
Examples
Let’s look at some examples to illustrate the process:
- Linear equation: y = 2x – 3
-
- Set y = 0: 0 = 2x – 3
- Solve for x: 2x = 3, x = 3/2
- The x-intercept is (3/2, 0)
- Quadratic equation: y = x² – 3x + 2
-
- Set y = 0: 0 = x² – 3x + 2
- Use the quadratic formula:
x = (-(-3) ± √((-3)² – 4(1)(2))) / 2(1) - Simplify to get x = 2 and x = 1
- The x-intercepts are (2, 0) and (1, 0)
By mastering this process, students and professionals can easily identify x-intercepts, which has a significant role in graphing and analyzing functions. These points provide valuable information about equations and their graphical representations, helping to interpret the meaning and implications of various mathematical relationships.
-
How to Find X and Y Intercepts: Techniques for Determining Y-Intercepts
Setting X to Zero
To find the y-intercept of a function, one needs to determine where the line or curve crosses the y-axis. This process involves setting x to zero and solving for y. The y-intercept is the point where the graph intersects the y-axis, and at this point, the x-coordinate is always zero. This step is crucial because it represents the condition where the graph touches or crosses the y-axis.
Solving for Y
Once x is set to zero, the next step is to solve the equation for y. The method of solving depends on the type of equation:
- For linear equations (y = mx + b):
-
- Set x = 0
- Substitute 0 for x in the equation
- Solve the resulting equation for y
- For quadratic equations (y = ax² + bx + c):
-
- Set x = 0
- Substitute 0 for x in the equation
- Solve for y
Examples
Let’s look at some examples to illustrate the process:
- Linear equation: y = 2x + 1
-
- Set x = 0: y = 2(0) + 1
- Solve for y: y = 1
- The y-intercept is (0, 1)
- Linear equation: 3x – 2y = 12
-
- Set x = 0: 3(0) – 2y = 12
- Solve for y: -2y = 12, y = -6
- The y-intercept is (0, -6)
- Linear equation: 2x + 4y = 12
-
- Set x = 0: 2(0) + 4y = 12
- Solve for y: 4y = 12, y = 3
- The y-intercept is (0, 3)
- Quadratic equation: y = x² – 2x – 3
-
- Set x = 0: y = 0² – 2(0) – 3
- Solve for y: y = -3
- The y-intercept is (0, -3)
By mastering this process, students and professionals can easily identify y-intercepts, which has a significant role in graphing and analyzing functions. These points provide valuable information about equations and their graphical representations, helping to interpret the meaning and implications of various mathematical relationships.
Conclusion
Mastering the art of finding x and y intercepts equips individuals with a powerful tool to analyze and interpret mathematical functions. This skill has a significant impact on various fields, from economics to physics, enabling professionals to extract meaningful insights from graphs and equations. By following the step-by-step methods outlined in this guide, readers can confidently tackle problems involving intercepts, enhancing their ability to sketch graphs accurately and understand the underlying relationships they represent.
The knowledge gained from this guide serves as a foundation to build upon more advanced mathematical concepts. It opens doors to deeper understanding in algebra, calculus, and other areas where graphing plays a crucial role. As readers apply these techniques in real-world scenarios, they’ll find themselves better equipped to solve complex problems and make data-driven decisions. This newfound expertise not only boosts academic performance but also proves invaluable in professional settings where mathematical analysis is key to success.
Also Read: how to calculate standard error in excel
FAQs
-
- X and y intercepts are points where a graph crosses the x-axis and y-axis, respectively. They provide important information about the function’s behavior.
- How do I find the x-intercept of a linear equation?
- Set y to zero in the equation and solve for x to determine where the line crosses the x-axis.
- What is the process for finding the y-intercept of a quadratic equation?
- Set x to zero in the equation and solve for y to find where the parabola intersects the y-axis.
- Can I use Excel to find x and y intercepts?
- While Excel is primarily for data analysis, you can use it to plot graphs and visually identify intercepts, though manual calculation is often more precise.
- How do I find x-intercepts using the quadratic formula?
- Set y to zero, then use the quadratic formula: x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} to find the x-intercepts of the quadratic equation.
- Why are x and y intercepts important in graphing?
- They help determine where a graph intersects the axes, providing key points for sketching and understanding the function’s behavior.
- What if my equation is in standard form?
- For standard form equations like Ax + By = C, set x or y to zero to find the intercepts.
- How can I find x and y intercepts for exponential functions?
- For exponential functions, find the x-intercept by setting y to zero and solving for x. The y-intercept is the function value when x equals zero.
- Do x and y intercepts always exist for every function?
- Not all functions have x and y intercepts. For example, functions that do not cross the axes will not have corresponding intercepts.
- How can I check my work when finding intercepts?
- Double-check your calculations by substituting the intercepts back into the original equation to ensure they satisfy it.